こんにちは、ミントです
前回までに、行列の生成や操作を学びました
今回は、行列の演算をやりたいと思います
行列には、
- 行列積
- 転置
- 逆行列
- 固有値・固有ベクトル
- 特異値分解
など応用面からも、とても大事な演算があります
これらの演算をすべて1からプログラミングするとなると、それなりに大変です。Rには、これらの計算を関数を使うことで、カンタンに実行できるメリットがあります
(これらの演算は、線形代数の書籍などで数式を追いながら学ぶのがいいですが、ここではRの使い方を学ぶことに重点を置くので省きます)
本記事の概要
行列の基本情報をゲットしよう
まずは、行列の基本情報である、行列の「 次元 」「 列数 」「 行数 」を調べれるようになりましょう
説明する前に、今回つかう行列1、行列2をこのように作成しました
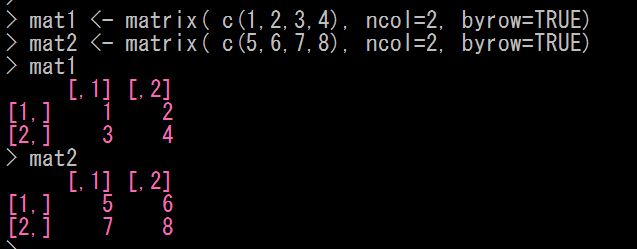
行列1の次元、行数、列数を求めてみます。それぞれ、
- 次元は、dim ( 調べたい行列オブジェクト名 ) 関数
- 行数は、nrow ( 調べたい行列オブジェクト名 ) 関数
- 列数は、ncol ( 調べたい行列オブジェクト名 ) 関数
を使います
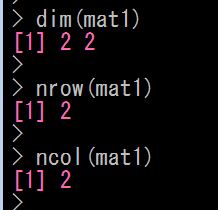
行列1の次元は2行2列、行数は2、列数は2、とわかりました
苦手な人もわかる、3つの行列のかけ算
行列には、3つのかけ算があります。これらを混同してしまうとよくないので、しっかり区別して理解してほしいと思います
(3つをすべて厳密にはかけ算とは呼べませんが、わかりやすいようにこのような表現にしています)
(1)、2つの行列の各要素どうしのかけ算
数学では、行列のかけ算は各要素どうしのかけ算ではありません
けれど、Rではそういう計算もサクッとできます
こんな感じです ↓
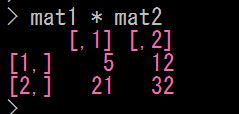
計算結果の1行1列の要素5は、行列1の1行1列の要素1と、行列2の1行1列の要素5のかけ算で、1 × 5 = 5 として計算されています。他の要素も同様です
(2)、行列のかけ算(行列積)
この「 行列積 」は、数学的に正しい行列のかけ算です
Rで実行するときは、「 %*% (パーセント・アスタリスク・パーセント)」 を使います
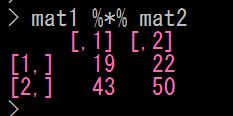
計算結果は、行列のかけ算の定義に従って計算されています
(3)、行列のかけ算(crossprod ( ) 関数)
Rでの行列積は、「 crossprod ( ) 関数 」 を使ってもできます
crossprod ( 行列1, 行列2 ) という形で使います
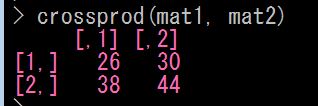
うん、できた!・・・あれ!?
(2)の結果と違う!!
なにか間違えたの!?
・・・
いえ、間違えてないんです
この crossprod ( ) 関数では、実はこのように計算しています
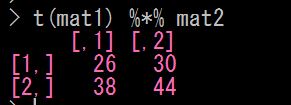
ん!? 「 t( ) 関数 」 ってのが使われてる!
「 t ( 行列オブジェクト名 ) 関数 」 は、行列を転置させる関数なんです(t はtranspose(転置)の略です)
行列の転置とは、その行列の行と列を入れ替えることを言います
たとえば、転置の操作では、1行2列の要素は2行1列の要素になり、2行1列の要素が1行2列の要素にします。これをすべての要素におこないます。このように、行列の対角項を中心にして、要素が入れ替わる操作のことを、転置と呼びます
crossprod ( ) 関数では、自動的に転置をしていて、それから行列積を計算しています。この点が(2)との違いになります
このように行列のかけ算は
- 「*」による行列の各要素どうしのかけ算
- 「%*%」による行列積
- 「crossprod ( ) 関数」による行列積
があり、これらを混同しないように気をつけましょう
行列の演算、よくつかう3つのアルゴリズム
行列の演算では、よく使うアルゴリズムが3つあります。逆行列、固有値問題、特異値分解です。これらは1からプログラミングするとそれなりに大変ですが、Rではカンタンに計算できるように関数が用意されています。(アルゴリズムの詳細などはここでは省きます)
(1)、逆行列
逆行列を求めるには、「 solve( ) 関数 」を使います
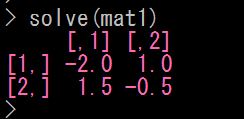
カンタンに計算できます
(2)、固有値問題
固有値・固有ベクトルを求めるには「 eigen ( ) 関数 」を使います
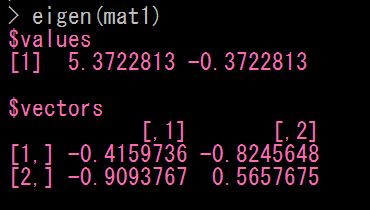
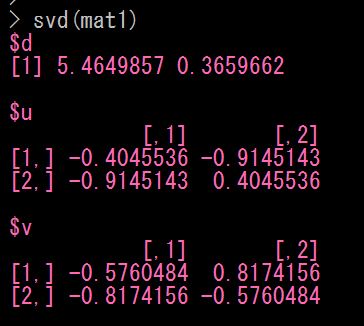
(3)、特異値分解
特異値分解は、「 svd ( ) 関数 」を使います
というわけで、今回は、行列の演算について、かけ算、逆行列、固有値問題、特異値分解などを学びました
Rには、「アレイ」という配列のデータ構造があります↓
こちら無料で読めます↓


