今日は「フラクタル」についてです
フラクタルってどっかで聞いたことあるけど、
フラクタルってなに?って方も多いと思います
本記事の概要
フラクタルは、私たちの周りにたくさんあります
有名な例としては、地形があります
ある場所を調べるときには、Google Mapなどで検索して、拡大・縮小をして見やすいようにしてたことがあるかと思います
千葉県の海岸をみてみたのがこちらです↓
赤で囲んだ海岸線の形に注目してください
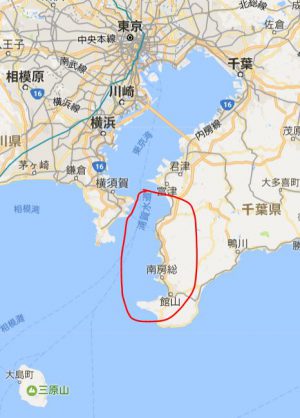
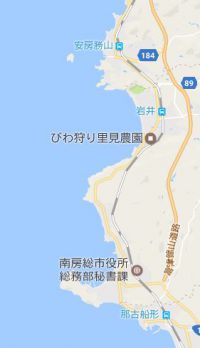
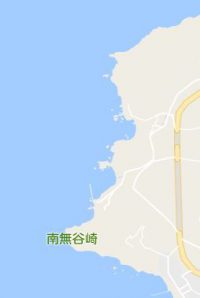
この写真がなんなの?同じところでしょ?って思われるかもしれません
実はこの3枚の写真、、縮尺がそれぞれ約10倍違っています
- 1番上の写真を10分の1にしたのが2枚目
- 2枚目をさらに10分の1にしたのが3枚目
- 1番上の写真を100分の1にしたのが3番目の写真
になります
縮尺がぜんぜん違うわけです
1番上の写真の赤で囲んだ部分と、残りの2枚の海岸線の形を比べてみてほしいんです
縮尺が大きく違うのに、形が似ていませんか?
もちろん厳密に同じ形ではないですが、おおまかな凸凹が同じようにあるのがわかると思います
縮尺が10倍・100倍と変わっても、形には共通の特徴があることがわかります
このような状況を、「自己相似」と呼びます
自己相似とは、自分自身に、自分自身と同じ形の小さな部分が含まれていることを表現した用語です
そして、フラクタルには自己相似という特徴があります
なので、雑駁な言い方ですが、フラクタルとは、自分の中に自分と似たより小さな(大きな)形を持つもの、といえます
フラクタルと、他の図形との違いは?
じゃあわたしたちが、学校で習ってきた図形となにが違うの?って思うかもしれません
三角形や四角形、円や球など、数学で習ってきましたよね
これらとフラクタルの違いは、
たとえば円では、その性質は半径という「長さ」で特徴づけることができます
四角形も辺の長さで形を特徴づけることができますよね
これらの図形では、「長さ」によって特徴づけられるわけです
一方、フラクタルでは、このような長さで特徴づけすることができません
なので、わたしたちになじみが深い、三角形や円などの図形と,
フラクタルとの違いは、長さで特徴づけできるか・できないか、といえます
このことから、フラクタルというのは、わたしたちが学校で習ってきた図形とは一風変わったものになっています
フラクタルのほかの例としては、「株価の変動」なども関係があります
新聞でもネットのページでも、金融関係のページを開くと、ギザギザの株価グラフが載っていますよね、こんなグラフです↓
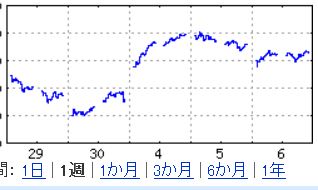
横軸が1日とか1週間とかを見ることが多いんじゃないでしょうか(この図の横軸は1週間のものです)
じゃあこの株価のグラフを、1年や3年単位というように、横軸のスケールを大きく変えてみたらグラフの形はどうなってるでしょうか
実は、1日や1週間のグラフと同じようなギザギザのグラフになっています
先ほどの地図の縮尺を変えたときと同じで、株価のグラフにも「自己相似」という性質があるんです
その辺は、こちらの本にくわしく書かれています
このように、私たちの社会の中にもフラクタルの性質が存在しています
私たちの生活の中には、まだ見つかっていないフラクタルがあるかもしれません
フラクタルってなんか面白そう!って思った方もおられるのではないでしょうか
フラクタルの父「マンデルブロ」
フラクタルという言葉を作ったのは「マンデルブロ」で、それが1975年になります
意外にあたらしい概念です
マンデルブロはこの業績で賞を受賞するなど認められた半面、
学術界ではポジションが得られず辛酸をなめた経験もしています
そういったマンデルブロの数奇な人生は自伝が出版されてたりもします
今回は、フラクタルを学んでみたい初学者の方向けに、フラクタルの全体像をサクッと学べる本をご紹介します
マンデルブロのフラクタル幾何学を邦訳した、数学者の広中平祐教授も推薦している1冊です。
わかりやすくて、フラクタルがどんなものなのか概観をつかむのに最適です。
フラクタルを学ぶのがはじめてのあなたには特におすすめです
本書の構成は以下の通りです
1、フラクタルとは何か?
1-1、特徴的な長さ
1-2、フラクタル
1-3、フラクタル次元
1-4、基本的なフラクタル
カントール集合と悪魔の階段
シルピンスキーのギャスケット
ド・ウィースのフラクタル
レビのダスト
tea time ミクロとマクロ
2、自然界のフラクタル
2-1、地学関係
地形
川
地震
2-2、生物関係
肺や血管の構造
植物の構造と虫の数
2-3、宇宙関係
星の空間的分布
クレーター、小惑星の直径分布
土星の輪
2-4、物理化学関係
固体表面
凝集体
放電パターン
高分子
相転移(パーコレーション)
乱流
ランダムウォーク
緩和過程(アモルファス・高分子)
ジョセフソン接合
分子のスペクトル
2-5、その他の分野
1/f雑音
通信系のエラー
所得の分布
株価の変動
ジップの法則
tea time フラクタルもどき
3、コンピュータのフラクタル
3-1、凝集体
3-2、カオスと写像
奇妙なアトラクター
写像によるカオス
写像によるフラクタル
3-3、ランダムクラスター
パーコレーション
スピン系のクラスター
3-4、放電と破壊のパターン
3-5、ランダムウォーク
3-6、オートマトン
3-7、パソコンのプログラムリスト
コッホ曲線
レビのダスト
凝集体
ローレンツ系
へノン写像のアトラクター
ジュリア集合
パーコレーション
自己回避ランダムウォーク
オートマトン
非整数ブラウン運動
4、理論的なフラクタルモデル
4-1、乱流モデル
4-2、フラクタル上のランダムウォーク
スペクトル次元
ロングタイムテイル
4-3、悪魔の階段
tea time 学会と研究会
5、フラクタルを扱う数学的方法
5-1、くりこみ群
5-2、安定分布
5-3、次元解析
5-4、非整数階の微積分
tea time 安定分布
6、フラクタルの拡張と注意
6-1、フラクタル次元の拡張
6-2、種々の次元のまとめ
6-3、時系列データの処理の方法
6-4、数学的補足
ハウスドルフ次元の求め方
ルベーグ測度とハウスドルフ測度
カントール集合のもつある性質
トポロジカル次元の定義
Dqの微分同型変換不変性
フラクタル集合の直積、交わり、、射影
フラクタル集合の微分可能性
グラフのフラクタル次元について
フラクタルランダムウォークの性質
tea time フラクタル的世界観
参考文献
索引
となっています。
フラクタルを学んでみたい初学者向けの本です。非常にわかりやすく、フラクタルの全体像をサクッと学べる内容となっています。
フラクタルの概観をつかむ最初の1冊にもおすすめの本です
↓こちら無料で読めます


